Eigenbehavior and Symbols
Complex Systems Modeling
Modeling, Algorithms, and Informatics Group (CCS-3)
Los Alamos National Laboratory, MS B256
Los Alamos, New Mexico 87545, USA
e-mail: rocha@lanl.gov or rocha@santafe.edu
Citation: Rocha, Luis M. [1996]."Eigenbehavior and Symbols". Systems Research, Vol. 12 No. 3, pp. 371-384, 1996
This paper is aailable in Adobe Acrobat (.pdf) format. This html version may be missing some special symbols, which you can get with the pdf version.
Abstract: In this paper I sketch a rough taxonomy of self-organization which may be of relevance in the study of cognitive and biological systems. I frame the problem both in terms of the language Heinz von Foerster used to formulate much of second-order cybernetics as well as the language of current theories of self-organization and complexity. In particular, I defend the position that, on the one hand, self- organization alone is not rich enough for our intended simulations, and on the other, that genetic selection in biology and symbolic representation in cognitive science alone leave out the very important (self-organizing) characteristics of particular embodiments of evolving and learning systems. I propose the acceptance of the full concept of symbol with its syntactic, semantic, and pragmatic dimensions. I argue that the syntax should be treated operationally in second-order cybernetics.
Keywords: Self-organization, Organizational Closure, Semantic Closure, Eigenbehavior, Emergence, Evolutionary Systems, Complexity Theory, Natural Selection.
1 Eigenbehavior and Self-Organization
In "Objects: tokens for (eigen-) behaviors, Heinz von Foerster [1977] postulated the existence of solutions for an indefinite recursive equation based on Jean Piaget's recursive structure of implications describing an observer's account of an interaction between a subject and an object. This equation basically asserts that what is observed at one particular time (obst) is the result of a cognitive/sensory-motor operation (COORD) on the previous instance of observation (obst-1):
The particularity of this expression is that it is recursive and without any particular starting point, or initial conditions. Thus, any specific instance of observation will still be the result of an indefinite succession of cognitive operations. Infinity is used as the mathematical artifice to express the position that observables do not refer directly to real world objects, but are instead the result of an infinite cascade of cognitive and sensory-motor operations (subsumed in COORD) in some environment/subject coupling. The "solutions" (Oi) to this equation, which do not exist in a strict mathematical sense as the equation is not given initial conditions, are believed to represent a stability in the chain of COORD operations, that is, those values which maintain their structure (or operation, or function) when cognitive/sensory-motor operations are on them performed, again and again, as the equation pursues its indefinite recursive chain:
In other words, for a long succession of cognitive operations, the structure of obst does not change (frame of stability); when this happens, obst is called an eigenvalue and represented by Oi. It can also be said thateigen-values are self-defining, or self-referent, in their frame of stability, through the operator COORD _ implying a complementary relationship (circularity, closure) between eigenvalues and cognitive/sensory- motor operators: one implies, or defines, the other. "Eigenvalues represent the externally observable manifestations of the (introspectively accessible) cognitive [operations] COORD". [von Foerster, 1977, page 278]. Further, "Ontologically, Eigenvalues and objects, and likewise, ontogenetically, stable behavior and the manifestation of a subject's 'grasp' of an object cannot be distinguished." [von Foerster, 1977, page 280]. Eigenbehavior is thus used to define the behavior of autonomous, cognitive systems, which through the closure of the sensory-motor interactions in their nervous systems, give rise to perceptual regularities as objects [Varela, 1979, chapter 13].
"Eigenvalues are discrete (even if the domain of the primary argument obs[t] is continuous)". In other words, even if the domain of an observable is continuous, its cognitive representation through COORD operators into eigenvalues must be discrete. This is a result of the stability of eigenvalues in the recursive chain of cognitive operators, if an eigenvalue Oj changes its structure, thus ending the frame of stability, it will either revert to unstable structures (varying at each cognitive operation), in which case the eigenvalue representation is lost, or form another frame of stability with a new eigenvalue representation Oi (Oi may be equal to Oj in which case it is referred to as a stable eigenvalue). In summary, eigenvalues are discrete representations of observables maintained by the successive cognitive operations of a cognitive agent. Notice that the representations and their stability are specific to the particular cognitive operations and how they recognize observables, that is, these discrete representations exist only in relation to the very same operators that define them. Also, since in the frame of stability an eigenvalue is "immune" to the cognitive operators that define it, we can further assert that the eigenvalue also implies the operators. Any system, cognitive or biological, which is able to relate internally stable structures (eigenvalues) to constant aspects of its own interaction with an environment can be said to observe eigenbehavior. Such systems are defined as organizationally closed because their stable internal states can only be defined in terms of the overall dynamic structure that supports them and which they define. In other words, amongst the products of the system's operation, are the processes required produce the system itself [Pask, 1992]. Organizationally closed systems are also informationally open [Pask, 1992], since they have the ability to change their structure and thus produce novel classifications of their environments.
1.1 Complexity Theory and Emergent Representation
It is perhaps easier to think about these concepts in the modern terminology of dynamical systems and complexity theory. The coupling of many simple elements into a network allows the establishment of highly recursive dynamical systems which can observe a wide range of attractor behaviors. An eigenvalue of an organizationally closed system can be seen as an attractor of a self-organizing dynamical system. The global "cooperation" of the elements of a dynamical system which spontaneously emerges when an attractor state is reached is understood as self-organization [von Foerster, 1960; Haken, 1977; Forrest, 1991; Kauffman, 1993]. The attractor behavior of any dynamical system is dependent on the structural operations of the latter (say, the set of boolean functions in a boolean network). Speaking of an attractor makes sense only in relation to its dynamical system, likewise, the attractor landscape defines its corresponding dynamical system. Furthermore, attractor values can be used to refer to observables accessible to the self-organizing system in its environment, and thus perform environmental classifications (e.g. classifying neural networks). This classification capacity was identified in the cybernetic terminology as eigenbehavior. Naturally, and this is the crux of the constructivist position [Glanville, 1988], not all possible distinctions in some environment can be "grasped" by the self- organizing system: it can only classify those aspects of its environment/sensory-motor/cognitive interaction which result in the maintenance of some internally stable state or attractor (eigenvalue). In other words, not everything "out there" is accessible; only those things that a particular physiology canconstruct with the stabilities of its own dynamics are.
A classifying self-organizing system is autonomous if all structural processes that establish and sustain its dynamics are internally produced and re-produced over and over again. Autonomy was previously referred to as organizational closure. A computational neural network by itself can classify an environment, but the processes (e.g. a backpropagation algorithm) that make it improve its classifying ability are external to the network. In this sense, the network itself is not autonomous, though the network together with the algorithm that changes its structure may be argued to be. It is precisely the ability of an autonomous system to change its structure in order to better classify a changing environment that defines emergent representation. For a classifying self-organizing system to change its classification ability, structural changes must be performed to alter its attractor landscape (this point is developed ahead). When the structure responsible for a given dynamics is changed, we obtain a new environmental classification (e.g. weight changes in a neural network). This process of obtaining novel classifications of an environment, by an autonomous self-organizing system, can be referred to as emergent classification (informational openness above). Emergent because it is the result of the local interaction of the basic components of the self-organizing system and not from a global controller. This bottom-up definition of emergence [Langton, 1989] is generally accepted in artificial life and connectionist artificial intelligence as the guiding conceptual framework of models of life and cognition. However, and following Cariani [1989] and Pattee [1986], I will adopt a stricter sense of emergence requiring the definition of a semantic level of description to be discussed in section 2.
The relationship between the terminologies of complexity theory and second-order cybernetics outlined above may be seen in some quarters as commonsensically simple. Most of the cybernetic principles of self-organization as defined by von Foerster and other participants of his program of research at the Biological Computer Laboratory in Urbana, Illinois in the 1960's and 1970's, were proposed within larger philosophical frameworks, with important implications for cognitive science and biology. In any case, the empirical basis for those theories depends on material and computational systems with the self-organizing characteristics outlined above. It is this empirical foundation of self-organization that I am exploring here, and not the related higher level interpretations of eigenbehavior.
1.2 Constructivism
Autonomous systems must construct their reality by using stable structures internally available. Objects are constructed by peculiarities of cognitive operators (the maintenance of stable structures) and are not accessible through a direct representation of real world categories. Constructivism, the philosophical cornerstone of second-order cybernetics, does not merely entail the idea that objects are not accessible but that objects are constructed by cognition and constitute its basic building blocks. Today, most of us agree with this in principle. However, what must still be addressed is how do these stable eigenvalues become eigenbehaviors, in other words, what is the nature of the structural coupling (to use the autopoietic terminology [Maturana and Varela, 1987]) between an autonomous, self-organizing system, and its environment? How do the internally constructed eigenvalues refer to aspects of the environment? How can we increase the variety of eigenbehavior? Can this variety be open-ended?
2 Emergence and levels of description
There are three levels that need to be addressed when dealing with the notion of emergent phenomena in self-organizing systems, in particular, of emergent classification. First, there is the material, dynamical, substrate which is the causal basis for all other levels that we may further distinguish. Second, we have the attractor behavior of this dynamics. Finally, we have the (possible) utilization of the set of attractorsas referents for some aspects of the interaction of the dynamical system itself with its environment (e.g. the pattern recognition abilities of neural networks).
2.1 Emergence and Explanation
Robert Rosen's concept of emergence defines it as the deviation of the behavior of a natural system from a model of it [Rosen, 1985, 1995]. Peter Cariani [1989] has developed this notion and named it emergence relative to a model. I see emergence relative to a model as an observer's switching between different models offering different modes of explanation. As Howard Pattee [1978] has pointed out, due to the subject-object or observer-system dichotomy, a given observed phenomenon possesses several modes of description, none of which provides a full explanatory power. In other words, models of physical phenomena explain only certain aspects of them, and to increase our understanding of the world we need complementary, at times irreducible, modes of description. Second-order cybernetics, through the work of Heinz von Foerster, has identified two main modes of description, the level of operations and the level of observations.
Returning to the issue of self-organizing systems and emergence, we observe that the level of attractor behavior is emergent to the dynamics because it cannot be explained solely by a description of the latter. Stability of dynamical states is not expressed in the language of the interactions between the components of a dynamical system. At this lower level, there is no distinction between a stable and an unstable state, between attractor and transient states. For instance, the transition rules of Conway's Game of Life cannot describe what "blinkers" and "gliders" are. Likewise, when the attractor landscape is utilized to classify an environment, a new level is created to define the representations necessary for this classifying function: a semantic relation is created. This self-organizing classification is emergent to the attractor landscape level since the latter can only describe stabilities of the dynamics and not any "standing for" relation with the environment. To continue with the previous example, the level of attractor behavior describes what a glider or a "glider gun" is in the Game of Life, however it cannot describe streams of gliders as information carriers in a universal computer built out of Life patterns [Poundstone, 1987]. The utilization of a glider as a bit of information requires a semantic relation imposed on the level of attractors. In second-order cybernetics, the lower levels of dynamics and attractor behavior are associated with the level of operations, while emergent representation is associated with the level of observations.
2.2 Semantic Emergence
No physical or formal description of the dynamical system and its attractors alone will completely explain the "standing-for", or semantic, dimension [Pattee, 1995a]. In figure 1, this third semantic level is represented through a triangle whose left corner stands for a dynamic attractor, the right corner represents the world "out there", and the top corner represents the system of representation (denoted by a question mark) by virtue of which an internal attractor can be related to its environment. It is also a system of reference, as the representational link between dynamic attractors and an environment is established in reference to a third component. This system defines a cut between what is internal and external to the system [Medina- Martins and Rocha, 1992], between the "knower" and the "known", that is, it defines an epistemic cut [Pattee, 1995b]. We have then environmental events and a system's representation of those, by virtue of some representational relation.
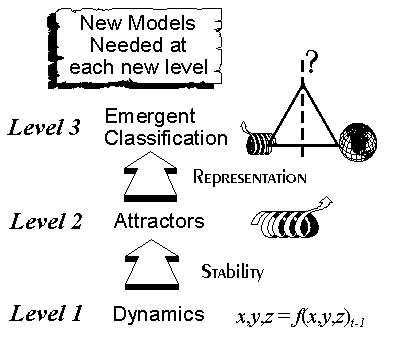
The emergence of level 2 (attractor behavior) from level 1 (dynamics) and of level 3 (classification) from level 2 is based on explanatory emergence defined above as the existence of complementary modes of description. However, the emergence of classification from attractor behavior introduces a more specific form of emergence as it establishes a representational relation between the classifying system and its environment. The recognition of this semantic emergence is precisely what gave rise to the second-order cybernetics movement. The object of systems research switched from the cybernetics of observed systems to the cybernetics of observing systems, that is, systems that construct their own representations of an environment through their own measurement of it.
To study these systems von Foerster proposed a theory of participant observation leading precisely to the formulation of eigenbehavior depicted earlier. One of the results in practice of this theory has been the division of the study of cognitive and biological systems into two distinct levels: dynamics (operations) and meaning (observations). All things material pertain to the former and left to the explanatory mechanisms of self-organization, while all things functional, semantic or symbolic pertain to the latter and studied as constructions of the subjective engagement of a participant observer. Curiously, self- organization itself is accepted as the only conceptual tool valid for the study of the level of operations which can thus be objectively observed. If we are participant observers of the world, then not only is semantic behavior constructed, but so is self-organization. Attractors, eigenstates, or symbols are equally constructed by us observers. Ultimately, all models are subjective. Having accepted this, we can now go our way trying to establish models and explanations that can be consensually agreed by as many observers as possible. I believe that some kinds of observing systems such as biological and cognitive systems, possess characteristics which are at the level of operations beyond mere self-organization and effectively symbolic. The syntactic part of this symbolic dimension can be, in fact must be, operationally defined, if we are to fully understand such systems. Their semantic dimension is still what makes them observing systems and treatable within a second-order cybernetics framework. Both dimensions should be acknowledged and pragmatically evaluated by their ability to classify relevant phenomena in a given environment. I expand on these ideas next.
3 Memory and Selected Self-Organization
3.1 Structural Change and Emergent Classification
Self-organizing approaches to life (biological or cognitive), in particular second-order cybernetics, sometimes take chaotic attractors as the mechanism which will be able to increase the variety (physiological or conceptual) of self-organizing, classifying, systems. External random perturbations will lead to internal chaotic state changes; the richness of strange attractors is converted to a wide variety of discriminating power. Dynamic systems such as neural networks clearly have the ability to discriminate inputs. Generally, the attractors of their dynamics are used to represent events in their environments: depending on inputs, the network will converge to different attractors. However, for any classification to have survival value, it must relate its own constructed states (attractors) to relevant events in its environment, thus, similar events in the world should correspond to the same attractor basin. Chaotic systems clearly do not have this property due to their sensitivity to initial conditions.
Chaotic classifications cannot grasp an ordered interaction with an environment, while point attractorsand simple limit cycles may not allow enough behavior change for a good increase in variety. The edge of chaos [Langton, 1990; Kauffman, 1993] regime seems to offer a good, intuitive, compromise. However, whatever the regime of a dynamic system, self-organization alone cannot escape its own attractor behavior. A given dynamic system is always bound to the complexity its attractor landscape allows. Even a strange attractor, though undoubtably endowed with a much richer variety of behavior than limit cycles or point attractors, is restricted to a small volume of the state space of the respective dynamic system. If the classification variety of the self-organizing system is restricted to such small volumes, then the ability to classify a changing environment is severely constrained.
For a dynamic system to observe genuine emergence of new classifications, that is, to be able to accumulate useful variations, it must change its structure. Creativity can only be attained by structural perturbation of a dynamical system. One way or another, this structural change leading to efficient classification (not just random change), has only been achieved through some external influence on the self-organizing system. Artificial neural networks discriminate by changing the structure of their connections through an external learning procedure. Evolutionary strategies rely on internal random variation which must ultimately be externally selected. In other words, the self-organizing system must be structurally coupled to some external system which acts on structural changes of the first and induces some form of explicit or implicit selection of its dynamic representations: selected self-organization.
Explicit control of a classifying system's structure would amount to the choice of a particular dynamics for a certain task and can be referred to as learning. Under implicit control, the self-organizing system is subjected to some variation of its structure which may or may not be good enough to perform our task. Those self-organizing systems which are able to perform the task are thus externally selected by the environment to which they are structurally coupled. If reproduction is added to the list of tasks these systems can produce based on their dynamic memories, then we have the ingredients for natural selection: inheritable variation and selection.
3.2 Distributed Memory
The dynamical approach of von Foerster [1965] to cognition emphasized the concept of memory without a record. By utilizing functionals to change the functions of state-determined systems, von Foerster formalized the idea that memory can be observed in systems which are able to change their own structure and therefore its dynamics and attractor behavior. Today, we name this kind of memory distributed, and the kind of models of memory so attained as connectionist. The categories a distributed memory system classifies are not stored in any particular location, they are nowhere to be found since they are distributed over the entire dynamics established by some network of processes [van Gelder, 1991]. They exist however in the form of attractors (eigenstates) which are nonetheless discrete as observed by von Foerster in section 1. Categories are not stored in any particular location of the network, but are identified with particular dynamic attractors, for which we need an emergent level of description as discussed earlier.
Now, for a self-organizing system to be informationally open, that is, for it to observe emergent classification of its own interaction with an environment, it must be able to change its structure, and subsequently its attractor basins explicitly or implicitly. Whatever the form of selection, this kind of self- organization must be able to classify its interaction with an environment by utilizing its distributed memory. For selection to occur we must have some internal vehicle for classification _ there must be different alternatives. The attractor landscape, or eigenvalues, offer these vehicles. This form of self-organization can be referred to as distributed memory selected self-organization. What is yet to be discussed is the potential of this kind of self-organization for efficient, open-ended variety.
Perhaps the most important characteristic of this distributed memory selected self-organization is the fact that its specific dynamics both constructs the classification of the environment and ultimately defines selection. That is, distributed memory cannot classify everything, only those aspects of the environment that create internal stabilities. Also, selection eventually acts on the functional characteristics of the dynamics (desired for some task) and not on memory itself. The consequence of this fact for biological systems is that natural selection (acting on this form of self-organization) is not free to evolve any organism, but it is constrained by the dynamic properties of the materiality of the organisms it acts upon _ evolution with both a self-organizing and selection component. The consequence for cognitive systems, is that what can be classified is also constrained by the particular materiality of the classifying system at stake _ not everything "out there" can be grasped. In other words, the particular self- organizing dynamics of a particular classifying system constrains the universe of its classification. However, we should look into how can this process be made more efficient, and allow for genuine open- ended emergence of variety in classification.
4 Descriptions and Symbols
4.1 Von Neumann and Description-Based Selection
Von Neumann [1966] defended that a threshold of complexity exists, before which complexity degenerates, and after which complexity can increase in an open-ended fashion. He proposed a self- replicating scheme based on the notion of a memory-stored description φ(A) that can be interpreted by a universal constructor A to produce A itself. In addition to the universal constructor, an automaton B capable of copying any description, φ, is included in the self-replication scheme. A third automaton C is also included to effect all the necessary manipulation of descriptions. To sum it up, the self-replicating system contains the set of automata (A + B + C) and a description φ(A + B + C); the description is fed to B which copies it and to A which constructs another automaton (A + B + C); the copy is then handled separately to the new automaton which together with this description is also able to self-reproduce. If the description of the self-reproducing automata is changed (mutated), in a way as to not affect the basic functioning of (A + B + C) then, the new automaton (A + B + C)' will be slightly different from its parent. Von Neumann used a new automaton D to be included in the self-replicating organism, whose function does not disturb the basic performance of (A + B + C); if the D part of the description mutates, say to D', then the system (A + B + C + D) + φ(A + B + C + D') will produce (A + B + C + D') + φ(A + B + C + D').
Notice that changes in (A + B + C + D%) are not heritable, only changes in the description, %(A + B + C + D%) are inherited by the automaton's offspring and are thus relevant for evolution. This ability to transmit mutations through descriptions cast in separate memories is precisely at the core of the principle of natural selection of modern Darwinism. Through variation (mutation) of memories, populations of different organisms are produced; the statistical bias these mutations impose on reproduction rates of organisms will create survival differentials (fitness) on the population which define natural selection. In principle, if the language of description is rich enough, an endless variety of organisms can be evolved. This is what open-ended emergent evolution means. This point needs to be further elaborated.
4.2 Descriptions require a Symbol System
Von Neumann's model clearly does not rely on a distributed but on a local kind of memory. Descriptions entail a symbol system on which construction commands are cast. These commands are not distributedover patterns of activation of the components of a dynamic system, but instead localized on "inert" structures which can be used at any time _ a sort of random access memory. By "inert" I mean material structures with many dynamically equivalent states, in other words, the semantic relation, or what the structures are used to refer to, must possess a large degree of arbitrariness so that certain representations are not much more probable than others. In the genetic system, most any sequence of nucleotides is possible, and its informational value is almost completely independent of the particular dynamic behavior of DNA or RNA. Notice that according to Von Neumann's own formulation, a symbol system utilized for the construction of self-reproducing systems is not an isolated artifact. Rather, in the context of construction, a symbol system entails a set of available parts. That is, construction blueprints are cast on a symbol system whose primitives are a finite set of parts. In the case of self-reproducing automata, these parts are "and", "or" and other logical operators, and in the case of the genetic code the parts are the set of aminoacids (the symbols are codons or sets of 3 nucleotides). It is in this sense that open-ended evolution must be understood. A given material symbol system cannot represent everything, only what its primitive parts can construct. Natural selection is open-ended for any form that can be constructed through folding aminoacid chains.
4.3 The Symbolic Advantage
Why then is there an advantage of local memory over distributed memory self-replication? Von Neumann's argument maintains that if we do not have symbolic descriptions directing self-replication, then an organism must replicate through material self-inspection of its parts. In other words, the dynamics must be able to produce copies of itself by template identification of parts existing in its environment. The simplest way would be to have every part of the structure individually heritable. Clearly, as systems grow in complexity, self-inspection becomes more and more difficult [Pattee, 1995a]. The existence of a language, a symbol system, allows a much more sophisticated form of communication. Functional, dynamic structures do not need to replicate themselves, they are simply constructed from physically non- functional (dynamically inert) descriptions. For instance, for an enzyme to replicate itself, it would need to have this intrinsic property of self-replication "by default", or it would have to be able to assemble itself from a pool of existing parts, but for this, it would have to "unfold" so that its internal parts could be reconstituted for the copy to be produced [Pattee, 1995a]. With the genetic code, however, none of these complicated "gimmicks" are necessary: functional molecules can be simply folded from inert messages. This method is by far more general since any functional molecule can be produced from a description, not merely those that either happen to be able to self-reproduce, or those that can unfold and fold at will to be reproduced from available parts. The evolution of distributed memory based self-organizing systems is restricted to this type of trivial (in von Neumann's sense) reproduction or to self-inspection based (self- description [Kampis, 1991]) reproduction.
The symbol system, with its utilization of inert structures, opens up a whole new universe of functionality which is not available for purely dynamical self-replication. In this sense, it can evolve functions in an open-ended fashion. Language has likewise opened up a whole new universe of meaning for cognitive systems, as they can access the dynamics of classification beyond local interactions. That is, communication between individuals, as well as internally, is not restricted to only those things we can "show" or otherwise somehow physically mimic: the displacement of local observations. Language may be, as the genetic system, a method to point to and reach a particular dynamics necessary in a particular context. It may allow a (fairly) random access to an otherwise distributed memory, defining a more sophisticated system of structural perturbation. We can refer to this mechanism as description based evolution. Its power is obviously immense. It is however at odds with the notions of self-organization depicted previously. For the purely formal von Neumann scheme, all constructions are possible, that is, in principle, there is nothing a formal symbol system cannot describe in given set of primitive parts. Allclassifications, all functions, all morphologies can be attained from a finite set of parts by such a mechanism: open-endedness. In contrast, self-organization tells us that a given autonomous system will be able to classify or morphologically achieve only a (small) subset of all possible system/environment configurations; precisely those for which it can construct dynamic stabilities.
4.4 Symbols and Second-Order Cybernetics
It can always be argued that the random access memory the genetic system establishes, is nothing but complicated dynamics, and the symbolic dimension is just the result of our subjective observation. In other words, again the distinction between the levels of operations and observation in second-order cybernetics. However, the argument is also extendable to the dynamic level itself, since it too is constructed by our subjective observations. The genetic dimension has established a new hierarchical level in evolutionary systems [Laszlo, 1987] which allows a greater level of control of the purely self- organizing dynamics. Failing to recognize this emergent symbolic level, does not allow the distinction between self-organizing systems such as autocatalytic networks [Kauffman, 1993], from living systems whose genetic memory does not require larger and larger autocatalytic networks to develop more and more complicated morphologies. Distributed memory self-organization requires more ans more complicated gimmicks to increase the complexity of its organization. There is inherited memory, but it is severely constrained as discussed above.
The introduction of a symbolic dimension allows the definition, operationally, of a richer form of organization which should still nonetheless be treated within a second-order cybernetics framework. Indeed, the concept of symbol in semiotic terms includes three distinct dimensions: syntactics, semantics, and pragmatics. It is only the semantic part that pertains to the level of observations, the syntactic part can, and should, be treated operationally, allowing us to identify a taxonomy of different forms of organizations of observing systems. Pragmatics is eventually associated with the selection of organizations in an environment, grounding in effect the classifications of autonomous systems in this environment through adaptation. This semiotic interpretation has been explored in Rocha[1996a], and it is based on Pattee's [1982, 1995a] notion of semantic closure.
5 Semantic Closure and Observing Systems
The notion of description implies a self-referential linguistic mechanism. A description must be cast on some symbol system while it must also be implemented on some physical structure. Since many realizations of the same symbol system are possible, viewing descriptions only as physical systems explains nothing about their symbolic nature in the control of construction. When Von Neumann's universal constructor A interprets a description to construct some automaton, a semantic code is utilized to map instructions into physical actions to be performed. When the copier B copies a description, only its syntactic aspects are replicated. Now, the language of this semantic code presupposes a set of material primitives (e.g. parts and processes) for which the instructions are said to "stand for". In other words, descriptions are not universal as they refer to some material constituents which cannot be changed without altering the significance of the descriptions. We can see that a self-reproducing organism following this scheme is an entanglement of symbolic controls and material constraints which is closed on its semantics. Pattee [1982, 1995a] calls such a principle of self-organization semantic closure.
The principle of semantic closure entails symbolic messages that code for compounds of material parts, which will themselves self-organize. In the computational lingo of Artificial Life, we can say that there is not a linear mapping of coded messages to functional products, rather messages encode dynamic structures which are then left to their own devices as they self-organize. I have referred to this procedureas emergent morphology [Rocha, 1995c, 1996a] which also entails a contextual interpretation of messages in the production of self-organizing products. We can then think of semantic closure as a conceptual principle that includes both description based evolution and self-organization, in other words, it implies a description based harnessing of self-organizing structures: selected self-organization with local memory. Figure 2 presents a taxonomy of self-organization dependent on some kind of memory. Notice that distributed memory selected self-organization can achieve plenty of the characteristics of semantic closure I have been discussing, however, without the attributes of local memory, that is, the symbolic dimension of descriptions, we cannot achieve the sort of open-endedness discussed earlier, since construction is not arbitrarily mediated by a code system [Umerez, 1995], but dependent on only those structures that happen to be able to be communicated by template reproduction or self-inspection.
It is here that the emphasis on the symbolic level of open-ended evolutionary systems must be tamed. Strong Darwinism, has emphasized the nature of the symbolic description of living systems. However, semantic closure with its description based selected self-organization is not reiterating this position. The symbolic component of evolutionary systems is stressed, but the material, dynamic, self-organizing characteristics of matter are equally stressed. It is the ultimate inclusive approach which is neither reductionist nor dualist [Pattee, 1995a]. While it is maintained that a purely physical description of dynamics will not explain symbolic function (as several material systems may implement the same function), it is also maintained that different material structures will not have identical domains of potentially evolvable functions. The important idea is that evolution relies both on self-organization and selection, and only those self-organizing systems able to harness their dynamics to obtain a symbolic dimension can have open-ended evolutionary potential.
Furthermore, semantic closure is compatible with second-order cybernetics ideas. A semantically closed system is a system capable of performing its own measurements of an environment. It is an observing system following an extended version of von Foerster's [1969] cognitive tiles, which includes an operationally defined symbolic dimension [Rocha, 1994a, 1995b], interactively observed semantics, and pragmatic grounding in an environment. In a sense, semantic closure expands second-order cybernetics with a symbolic dimension. The semiotic treatment [Rocha, 1995c, 1996a] further constrains semantically closed systems by emphasizing selection according to the accuracy of their constructed classifications of an environment, thus establishing a selected form of self-organization based on local memory. Accepting these three semiotic levels of organization in biological and cognitive systems entails a position of evolutionary constructivism [Henry and Rocha, 1996; Rocha, 1996b] which emphasizes equally the act of construction of categories as well as their validity (fitness, degree of intentionality) in an environment. It also stresses the contextual dependence of categories on their dynamic interaction with an environment.
6 What does it mean in practice?
6.1 Genetic algorithms and development: self-organization and selection in Artificial Life
Lately much attention has been posited on evolutionary strategies that bring together self-organizing systems and natural selection inspired algorithms. Particularly in the field of Artificial Life, Kitano[1994],and Dellaert and Beer [1994], have proposed GA's which do not encode directly their solutions, but rather encode generic rules which develop into boolean networks simulating genetic regulatory networks. With these approaches, GA's no longer model exclusively selection, but also a self-organizing dimension standing for some materiality. The GA does not search the very large space of possible solutions, but a space of basic rules which can be manipulated to build different self-organizing networks. These networks are then started and will converge to some attractor behavior standing for a solution of our simulation. Rather than directly encoding solutions, the GA harnesses a space of possible self-organizing networks which will themselves converge to a solution _ emergent morphology. The computational advantage of these systems lies on the tremendous reduction of the algorithm's search space since the solutions do not have to be encoded in all details, the emergent morphology "takes care" of details we do not need to encode [Rocha, 1995c]. By simulating both selection and self-organization, the size of descriptions is dramatically reduced, and an avenue is opened for studying the simulation of both the symbolic and material aspects of evolutionary systems.
6.2 Categorization and Belief
Eleanor Rosch [1978] and George Lakoff [1987], among others, have stressed the importance of an embodiment of cognition to deal with its representation issues. In Rocha [1994b, 1995d, 1996b] I have introduced a set structure called evidence set based on fuzzy logic and the Dempster-Shafer [Shafer, 1976] theory of evidence. These structures allow the inclusion of all forms of uncertainty recognized in information theory [Klir, 1993] as well as a formalization of belief and contextual dependencies in a set format. Evidence sets are mathematical structures defined in two distinct levels: membership and belief. The first is associated with unconstrained syntactical representation, while the second constrains this representation within a mathematical framework of belief. Evidence sets have been proposed as higher level models of selected self-organization, and tools for models of cognitive categorization under evolutionary constructivism [Henry and Rocha, 1996; Rocha, 1996b]. They can also be useful in accounting the uncertainty of interval methods of reliable computation [Rocha et al, 1996].
7 Conclusions: selection meets self-organization and von Foerster
I have stressed that though von Foerster's formulation of the eigenbehavior of self-organizing systems with distributed memory represents a minimum requirement for evolutionary systems, their evolutionary potential is much larger if further endowed with dynamically "inert" structures to be used by their classification mechanisms. In other words, if eigenvalues are further endowed with a symbolic dimension, their evolutionary potential is open-ended. It was stressed that this by no means entails a return to purely symbolic approaches to cognition, nor a belief in the absolute sovereignty of natural selection in evolution. Rather, it is a call for more inclusive, hybrid approaches to such evolutionary and learning systems. This form of embodied coupling of a living/cognitive system to its environment shows that Heinz' legacy for the understanding of these systems is alive and kicking, and with extraordinary evolutionary potential
Acknowledgments
I would like to thank Heinz for one day picking up the phone in Pescadero, and so enthusiastically fostering the desire of young man, calling from the other side of the world, to know more about all these things. It never ceases to amaze me, the kindness and genuine interest Heinz posits on those who seek him. He once told me of his desire to see science become an affair between human beings. As far as I am concerned, he has always lived up to this humanistic reputation _ and a wonderful one at that.
References
Cariani, Peter [1989]. On the Design of Devices with Emergent Semantic Functions. Phd dissertation. Systems Science Department, Watson School, SUNY-Binghamton..
& nbsp; Dellaert, F. and R.D. Beer [1994]."Toward an evolvable model of development for autonomous agent synthesis." In: Artificial Life IV: Proceedings of the Fourth International Workshop on the Synthesis and Simulation of Living Systems. R. Brooks and P. Maes (Eds.). MIT Press.
Forrest, S. (Ed.) [1990]. Emergent Computation. MIT Press.
Glanville, R. [1988]. Objekte. Merve Verlag.
& nbsp; Haken, H. [1977]. Synergetics. Springer-Verlag.
Henry, C. and L.M. Rocha [1996]."Language theory: consensual selection of dynamics." In: Cybernetics and Systems '96. R. Trappl (Ed.). World Scientific Press. (In press).
Kampis, George [1991]. Self-Modifying Systems in Biology and Cognitive Science. .
Kauffman, S. [1993]. The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press.
Kitano, H. [1994]."Evolution of Metabolism for Morphogenesis." In: Artificial Life IV. Brooks, R.A. and P. Maes. MIT Press. pp 49-58..
Klir, George J. [1993]."Developments in uncertainty-based information." In: Advances in Computers. M. Yovits (Ed.). Vol. 36, pp 255-332.
Lakoff, G. [1987] Women, Fire, and Dangerous Things. Chicago University Press.
Langton, Christopher G. [1989]."Artificial Life." In: Artificial Life: SFI Studies in the Sciences of Complexity. C.G. Langton (Ed.). Addison-Wesley. pp. 221-249.
Langton, Christopher G. [1990]."Computation at the edge of chaos: phase transitions and emergent computation." In: Emergent Computation (Special Volume of Physica D Vol. 42). S. Forrest (Ed.). MIT Press, pp. 12-37.
Laszlo, E. [1987]. Evolution: The Grand Synthesis. New Science Library.
Maturana, H., and F. Varela [1987]. The Tree of Knowledge: The Biological Roots of Human Understanding. New Science Library.
Medina-Martins, Pedro R. and Luis Rocha [1992]."The in and the out: an evolutionary approach." In: Cybernetics and Systems Research '92. Robert Trappl. World Scientific Press. pp 681-689.
& nbsp; Pask, Gordon [1992]."Different kinds of Cybernetics." In: New Perspectives on Cybernetics. Gertrudis Van de Vijver (Ed.). Kluwer Academic Publishers. pp. 11-31.
Pattee, Howard H. [1978]."The complementarity principle in biological and social structures." In: Journal of Social and Biological Structures Vol. 1, pp. 191-200.
Pattee, Howard H. [1982]."Cell psychology: an evolutionary approach to the symbol-matter problem." In: Cognition and Brain Theory Vol. 5, no. 4, pp 325-341.
Pattee, Howard H. [1986]."Universal principles of measurement and language functions in evolving systems." In: Complexity, Language, and Life: Mathematical Approaches. J. L. Casti and A. Karlqvist (Eds.). Springer- Verlag. Reprinted in Klir[1991]. pp 579-592 .
Pattee, Howard H. [1995a]."Evolving self-seference: matter, symbols, and semantic closure." Communication and Cognition - AI Vol. 12, nos 1-2 (Rocha [1995a]). pp. 9-27 .
Pattee, Howard H. [1995b]."Artificial life needs a real eoistemology." In: Advances in Artificial Life. F. Moran, et al. Springer-Verlag. pp 23-38.
Poundstone, W. [1987]. The Recursive Universe. Oxford University Press.
Rocha, Luis M. [1994a]."Von Foerster's cognitive tiles: semantically closed building blocks for AI and Alife." In: Cybernetics and Systems ' 94. Robert Trappl (Ed.). Vol. 1, pp 621-628. World Scientific Press.
Rocha, Luis M. [1994b]."Cognitive Categorization revisited: extending interval valued fuzzy sets as simulation tools for concept combination." In: Proc. of the 1994 Int. Conference of NAFIPS/IFIS/NASA. IEEE. pp 400-404.
Rocha, Luis M. (Ed.) [1995a]. special issue in Self-Reference in Biological and Cognitive Systems. Communication and Cognition - Artificial Intelligence Vol. 12, nos. 1-2
Rocha, Luis M. [1995b]."Artificial semantically closed objects." Communication and Cognition - AI. Vol. 12, nos. 1-2 (Rocha[1995a]). pp. 63-90.
& nbsp; &n bsp; &nb sp;Rocha, Luis M. [1995c]."Contextual Genetic Algorithms: Evolving Developmental Rules." In: Advances in Artificial Life. F. Moran, A. Moreno, J.J. Merelo, and P. Chacon (Eds.). Series: Lecture Notes in Artificial Intelligence, Springer-Verlag. pp. 368-382.
Rocha, Luis M. [1995d]."Interval based evidence sets." In: Proc. of ISUMA-NAFIPS'95 IEEE Press, pp. 624-629.
Rocha, Luis M. [1996a]."Selected self-organization: from eigenbehavior to descriptions." In: Proceedings of the Int. Seminar on Evolving Systems, Vienna 1995. S. Salthe and G. Van de Vijver. MIT Press. (in press).
& nbsp; Rocha, Luis M. [1996b]."Relative uncertainty and evidence sets: a constructivist framework." In: International Journal of General Systems (In Press).
Rocha, Luis M., V. Kreinovich, and K. B. Kearfott [1996]."Computing uncertainty in interval based sets." In: Applications of Interval Computations. V. Kreinovich and K.B. Kearfott (Eds.). Kluwer, pp. 337-380.
Rosch, E. [1978]."Principles of Categorization." In: Cognition and Categorization. E. Rosch and B.B. Lloyd (Eds.). Hillsdale. pp. 27-48.
& nbsp; Rosen, Robert [1985]. Anticipatory Systems. Pergamon Press.
Rosen, Robert [1991]. Life Itself. Columbia University Press.
Rosen, Robert [1995] "The mind-brain problem and the physics of reductionism". Communication and Cognition - AI Vol. 12, nos. 1-2 (Rocha [1995a]), pp. 29-43.
Shafer, Glenn [1976]. A Mathematical Theory of Ev
